
Lorsque l’on souhaite faire des mesures de variables biophysiques dans une parcelle, il faut remplir deux objectifs principaux: obtenir une représentativité géographique de la parcelle (on doit prendre des mesures sur toute l’emprise) et assurer une représentativité statistiques des pixels de la zone étudiée.
Un indice de végétation peut être utilisé pour caractériser les pixels de la parcelle, dans notre cas nous utiliserons le NDVI (Normalized Difference Vegetation Index), et une classification Kmeans est faite afin de mettre en évidence les zones homogènes de la parcelle à partir des images Sentinel2 du programme copernicus
Représentativité géographique
Un bon moyen d’aller prélever partout dans la parcelle est de la diviser en carrés limités par les bords de la parcelles, la taille des cellules va conditionner le nombre de points de prélèvements que l’on choisira comme le centroïd de chaque cellule.
Dans la parcelle ci dessus, si l’on choisit 5 cellules alors le programme va superposer une grille de (5*5) cellules sur la parcelle, puis limiter les cellules aux bordures de la parcelle.
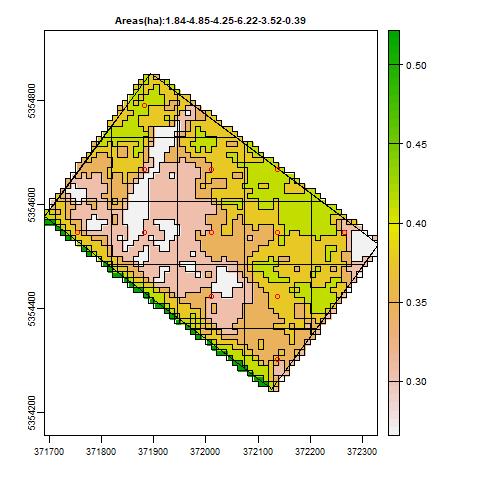
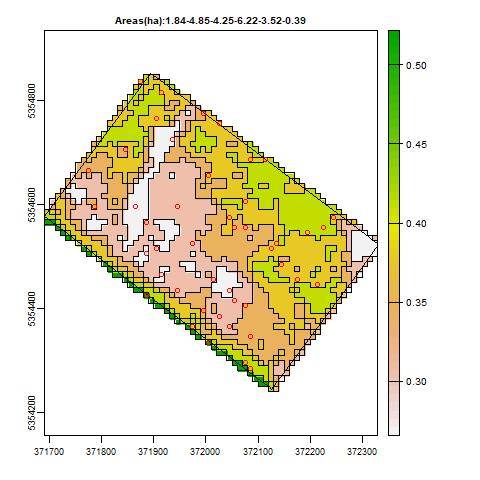
Sur l’image ci-dessus, on voit qu’il y a 6 classes de NDVI dans la parcelle, les surfaces de chaque classe sont indiquées dans le titre du graphique.
Les cercles rouges correspondent aux points de prélèvements. Il y en a ici une dizaine.
Représentativité statistique
L’objectif est donc de trouver le nombre de points GPS de prélèvements minimum qui caractérisera au mieux cette analyse fréquentielle. On doit donc respecter les critères moyenne, écart-type et distribution du nuage de point de la parcelle.
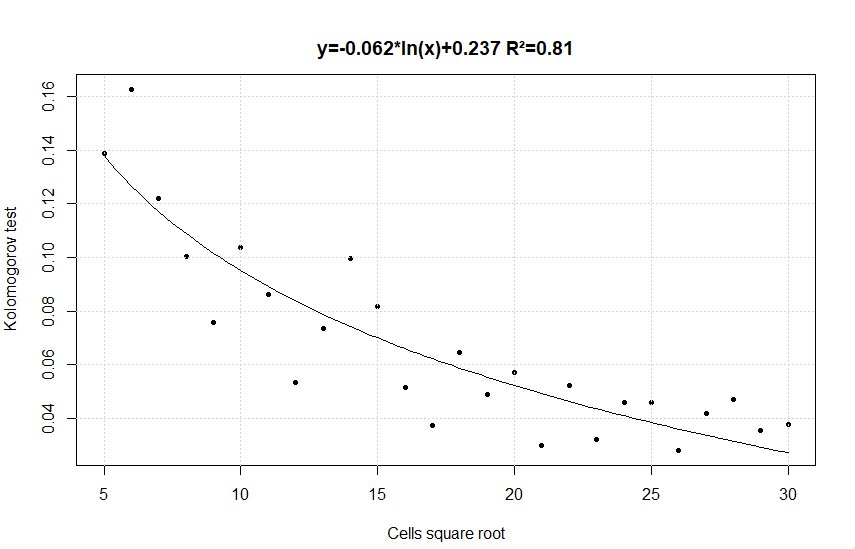
Pour ce faire on utilise le test de Kolmogorov-Smirnov qui mesure la distance maximum entre deux lois de répartition. Plus le résultat du test est petit plus la représentativité de l’échantillon est bonne.
On va donc, calibrer le nombre de cellules dans la parcelle de façon à avoir une qualité statistique inférieure à une valeur seuil, typiquement, on va partir d’un nombre de cellule bas, puis l’augmenter jusqu’à constater une dérivée de la fonction (Cellules/Résultat) proche de zéro, indiquant que le modèle ne s’améliore plus.
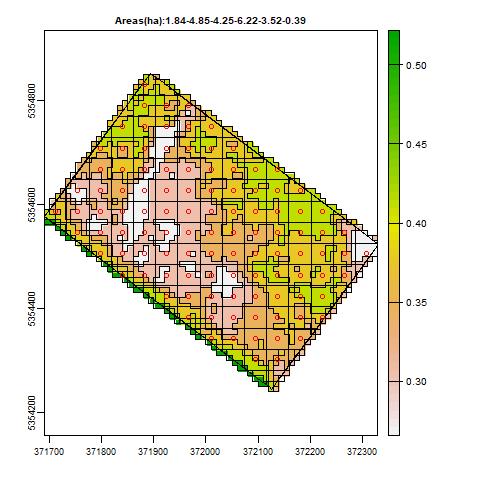
Sur l’image ci dessus on obtient donc un plan de prélèvements avec 108 points de mesures, la répartition géographique est évidemment parfaite avec la grille.
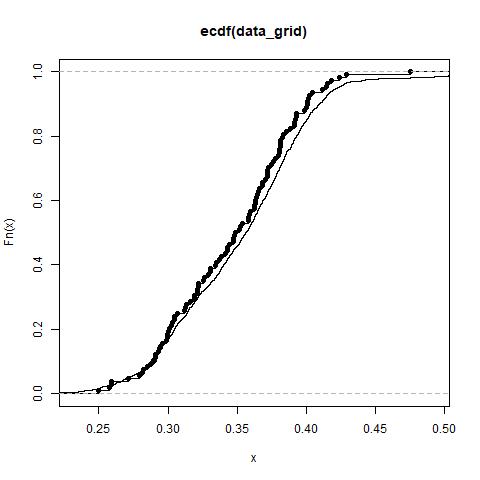
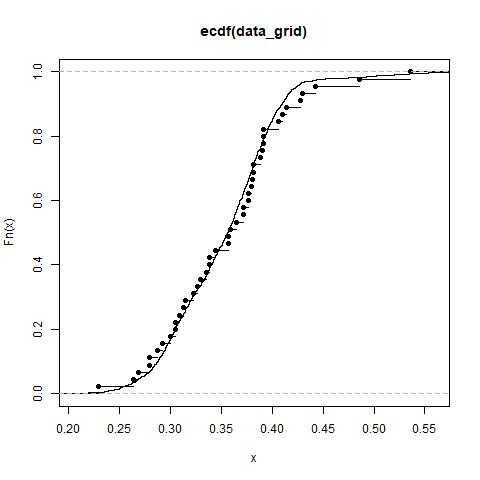
On constate que les deux jeux de données (pixels de la parcelle et points de prélèvements) se comportent de la même manière au vu de la fonction de répartition (fréquence cumulée fonction du niveau de NDVI)
La dernière étape consiste à exporter au format GPX les points de prélèvements pour aller faire les mesures dans la parcelle.
Comparaison avec une méthode aléatoire
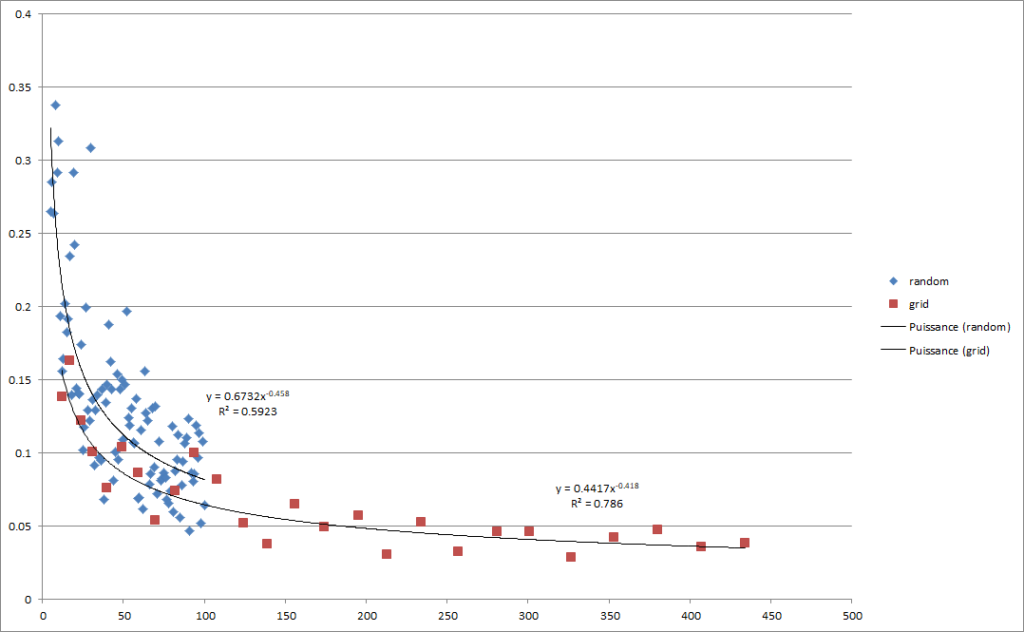
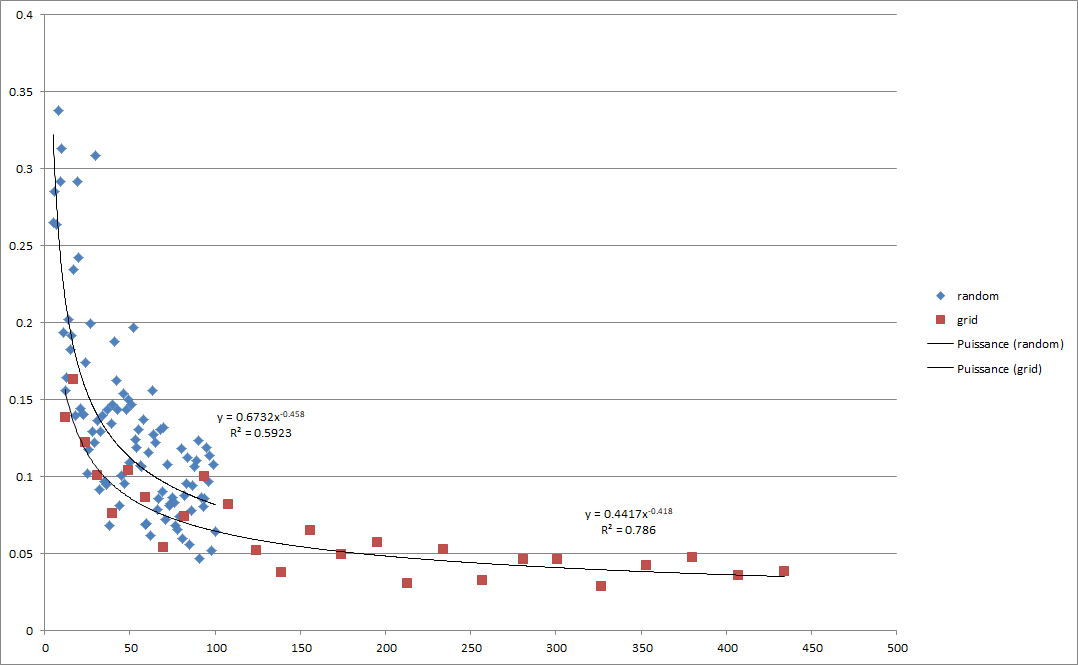
On constate sur le graphe ci-dessus, qu’au même nombres de point GPS la méthode de la grille donne un meilleur résultat que la méthode aléatoire au vu des deux régressions.
